Polynomial Functions
| Division Algorithm In this page we show how to divide one polynomial by another . We first explain what it means to divide one polynomial by another. Let 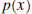 and and 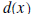 be two polynomials . To
divide be two polynomials . To
divide 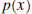 by by
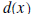 means to find two additional means to find two additional polynomials 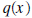 and and 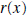 such that such that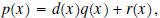 where the degree of 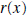 is less than the degree of is less than the degree of 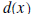 . The polynomial . The polynomial
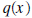 is called the quotient is called the quotientand the polynomial 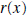 is called the remainder. is called the remainder.The polynomial doing the dividing, 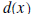 , is called the divisor, and the
polynomial being divided, , is called the divisor, and the
polynomial being divided, 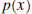 , is called , is calledthe dividend. |
| Example 1: Before looking at an example involving
polynomials, let’s look at an example involving integers. Divide 27 by 4. Solution : Remember, to divide 27 by 4, means to find two integers. The quotient, which tells us the largest number of times 4 goes into 27, and the remainder which tells us how much is left over. To find the quotient we list multiples of 4. 4, 8, 12, 16, 20, 24, 28 Looking at the list we see that the largest number of times 4 goes into 27 is six. The remainder is 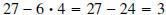 . Thus, we have . Thus, we have
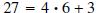 . The quotient is 6 and the
remainder is 3. . The quotient is 6 and the
remainder is 3. |
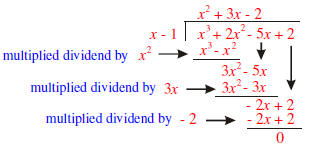
Example 2: Divide the polynomial
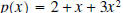 by
the polynomial by
the polynomial 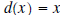 . .Solution: The first step is to write each polynomial so that the exponents are decreasing in size. 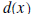 is isalready in that order, but we need to write 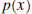 as as
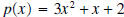 . The next
step is to display the two . The next
step is to display the twopolynomials as follows
What do we have to multiply x by to get 3x2? The answer is 3x. The entire procedure is shown below.
In a) we write 3x above the horizontal line,
because 3x times x equals 3x2; 3x2 is then subtracted from the
|
| Historical Comment: The use the word algorithm
means a step by step breakdown of a complicated mathematical procedure . The word comes from the name of a famous Islamic astronomer/mathematician,  , who is considered the founder of algebra. In fact the
word algebra comes from the title of a , who is considered the founder of algebra. In fact the
word algebra comes from the title of afamous book, Al-Jabrwa-al-Muqabilah, which was written by  . .Example 3: Divide the polynomial 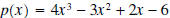 by the polynomial by the polynomial
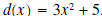 . .Solution: First a few observation about what the quotient and remainder have to look like. • The remainder is a polynomial of degree one or less because the divisor, 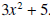 , is a polynomial of , is a polynomial ofdegree 2. The remainder is a polynomial of degree less than the degree of the divisor. Hence its degree is 1 or less. • The quotient is a polynomial of degree 1 because the leading term of the divisor is 3x2 and the leading term of the dividend is 4x3. Thus, we need to multiply 3x2 by 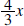 to get 4x3, and the degree of to get 4x3, and the degree of
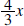 is is1. Another way to get this is to subtract the degree of the divisor from the degree of the dividend. • The computations are shown below:
• The row
|
Example 4: Divide the polynomial
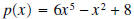 by
the polynomial by
the polynomial
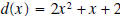 . .Solution: Before we show the details of the division process. Let’s see what we can surmise about the remainder and quotient. • The degree of the quotient is 3, because 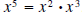 . The leading
coefficient of the quotient is 3 . The leading
coefficient of the quotient is 3because 6 equals 3 times 2. That is, 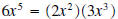 . .• The degree of the remainder is no more than 1, as the degree of the divisor is 2. It is possible that the degree is 0, but we can’t know for sure without doing the actual computations. • In the details below, notice that we included in the dividend the missing terms. That is the missing term x4 is included as 0x4, etc. This is done to help eliminate computational errors.
The quotient is |
Example 5: Divide
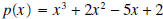 by by 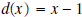 . .Solution: Notice that the degree of the quotient is 2 and its leading term is 1. The remainder must be a constant, since it will be a polynomial of degree less than 1.
The remainder is 0 and the quotient is
Notice that since the remainder is zero, the dividend is a multiple of the divisor. |
| Here we state the division algorithm for
polynomials, and discuss synthetic division . Synthetic division is a shorthand way to divide a polynomial by a polynomial of the form x - c. Note this last polynomial has degree 1 and its leading coefficient is also 1. Synthetic division is only used when the divisor is a polynomial of degree 1 with leading coefficient 1 also. The Division Algorithm Let 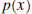 and and 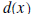 be any two polynomials. Then there exist unique
polynomials be any two polynomials. Then there exist unique
polynomials 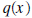 and and 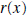 , ,where the degree of 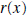 is less than the degree of is less than the degree of 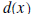 , such that , such that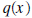 is called the quotient, is called the quotient, 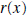 the remainder, the remainder, 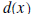 the divisor, and the divisor, and 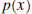 is called the dividend.
is called the dividend.In the previous pages we showed how to calculate the quotient and remainder. So the only thing new in the above statement is the uniqueness of the quotient and remainder. If the divisor is a polynomial of degree 1, with leading coefficient also 1, (the divisor is of the form x - c,) then there is a process called synthetic division which enables us to find the quotient and remainder fairly easily. In the example below we divide 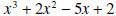 by the polynomial by the polynomial
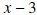 . In
fact we do the division twice. . In
fact we do the division twice.The first time using long division and the second time using synthetic division. |
Example 6: Divide
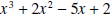 by by 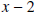 . .Solution:
The long division of
|
Suppose we divide 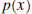 by x
- c, then the remainder
is a constant k, which may be zero, and we have the by x
- c, then the remainder
is a constant k, which may be zero, and we have theequality 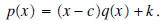 If we evaluate this equality at 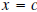 , we get , we get
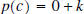 . .Ohhh, the remainder when 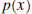 is divided by is divided by
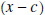 is is 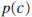 . This is
important, make sure you understand and . This is
important, make sure you understand andremember it. |
Question: If 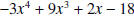 is divided by x
- 1,
what is the remainder? is divided by x
- 1,
what is the remainder?Answer: If 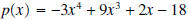 is divided by x - 1, the remainder is is divided by x - 1, the remainder is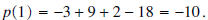 Question: If 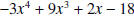 is divided by x + 1, what is the remainder? is divided by x + 1, what is the remainder?Answer: If 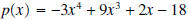 is divided by x + 1, the remainder is is divided by x + 1, the remainder is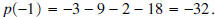 |
For complicated polynomials  if the value of if the value of
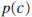 is desired it is sometimes easier to use synthetic division is desired it is sometimes easier to use synthetic divisionto calculate the remainder, and then use the fact that the remainder is 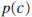 . Although, since we now have ready . Although, since we now have readyaccess to computers and calculators, evaluating polynomials is an easy task. Example 7: Using synthetic division, divide 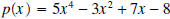 by by
Solution: We take notice that the degree of the quotient is 3 and that the x3 term is missing in 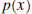 , but , butwe’ve included it below by placing a zero in the top row.
Thus, the quotient equals
|
Example 8: Using synthetic division divide
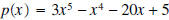 by by
Solution: We have to be careful here. Synthetic division assumes that we are dividing by x - c. So in this particular example 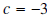 . .
The quotient equals
|
Example 9: Divide
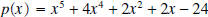 , by , by
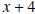 using synthetic division.
using synthetic division.Solution: Note that 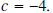
The quotient equals
|
| Prev | Next |
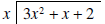
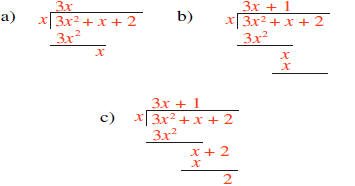
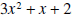 . The next
. The next 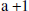 (see b)
is written above the horizontal
(see b)
is written above the horizontal and the
2 is brought down. The degree of the
and the
2 is brought down. The degree of the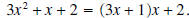
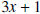 and the remainder is 2. This can also be
written
and the remainder is 2. This can also be
written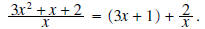
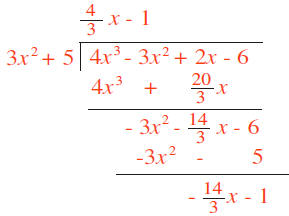
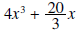 is obtained by multiplying
is obtained by multiplying 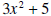 (the divisor) by
(the divisor) by
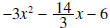 is obtained by subtracting
is obtained by subtracting
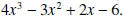
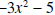 is obtained by multiplying
is obtained by multiplying
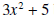 by -1, and the last row is
obtained by
by -1, and the last row is
obtained by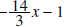 and the quotient is
and the quotient is
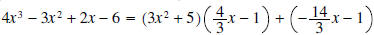 and
and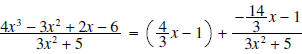

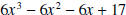 and the remainder is
and the remainder is
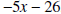 .
.
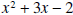 .
This can also be written as
.
This can also be written as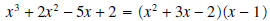 or
or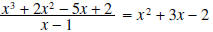
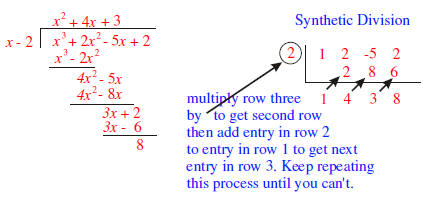
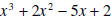 by
by
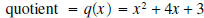 and
and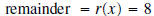

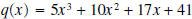 and
the remainder equals 74.
and
the remainder equals 74.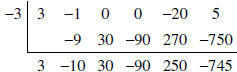
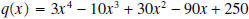 , the
remainder equals - 745, and
, the
remainder equals - 745, and 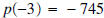 .
.
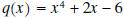 , the remainder
equals 0, and
, the remainder
equals 0, and