Point-Slope Formula
Writing an equation of a line using Point - Slope Formula
Here are two ways to derive the point-slope formula.
1. Suppose we have a line. Then we have
slope = m =
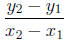
for any points on our line, (x1, y1) and (x2, y2).
In particular, suppose we have a point on our line, (x1,
y1), but we allow
a point (x, y) to be any other point on our line. Then the slope of our
line is given by
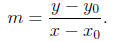
2. Begin with y = mx.
Example Use the point-slope formula to find an
equation of a line passing
through the point (2, 4) and having a slope of 1/6 . Write the answer in slope-
intercept form .
| 1. | (write the point-slope form) |
| 2. | ( solve for y ). |
Example Use the point-slope formula to find an
equation of a line passing
through the points (-1,-2) and (3, 2). Write the answer in slope-intercept form.
| 1. | (find slope) |
| 2. | (write the point-slope form) |
| 3. | (solve for y). |
Example Use the point-slope formula to find an equation of a line perpendicular to the line
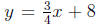
and passing through the point (1, 5). Write the answer in slope-intercept form.
| 1. | (find slope) |
| 2. | (write the point-slope form) |
| 3. | (solve for y). |
Example Use the point-slope formula to find an equation of a line parallel
to the line 2x-y = 1 and passing through the point (2, 3). Write the answer
in slope-intercept form.
| 1. | (find slope) |
| 2. | (write the point-slope form) |
| 3. | (solve for y). |
Summary of Different Forms of Linear Equations
| Form | Example |
| Standard Form: Ax + By = C | 3x - 8y = 5 |
| Horizontal Line: y = k, k constant | 3x - 8y = 5 |
| Vertical Line: x = k, k constant | 3x - 8y = 5 |
| Slope-Intercept Form: y = mx + b | y = 2/3x - 8 |
| Point-Slope Form: y - y1 = m(x - x1) | y - 3 = -2(x + 1) |
Definitions
•In an (xy)- coordinate system , the variable being predicted by the mathematical equation is called the dependent variable. It is represented by y.
•In an (xy)- coordinate system , the variable used to make
the prediction
is called the independent variable. It is represented by x.
Example Paper airplanes each cost 3 cents.
Therefore, an equation modeling
the cost, y, of x paper airplanes is given by
y = 3x.
1. Which variable is the independent variable?
2. Which variable is the dependent variable?
3. How much do 20 paper airplanes cost?
Example Baby Bill has 90 cents. He wants spend all
of his money on candy
and paper airplanes. The candy costs 5 cents and the paper airplanes cost 3
cents.
1. Make an equation representing this information. Let x
represent the
number of paper airplanes, and let y represent the number of candies.
2. Find and interpret the x - and y- intercepts.
3. Solve the equation for y. What sort of questions will
this slope intercept
equation help us answer?
4. If Baby Bill buys ten paper airplanes, how many candies
can he buy?
Example The following table represents the amount
of cheese burgers Tom
The Cat has eaten prior to the given dates. Let x represent the number of
years since 1970, and let y represent the amount of cheese burgers eaten.
| Year | amount of cheeseburgers eaten |
| 1970 | 250 |
| 1980 | 350 |
| 1990 | 450 |
| 2000 | 550 |
1. Make a graph that represents this data.
2. Find the equation of the line between the points (0, 250) and (30, 550).
3. What does the slope of the line represent?
4. Which is the independent variable?, Which is the dependent variable?
Example Tom the Cat decides to rent his catnip to
his brother. He charges
a 75 cent deposit and 25 cents per day (paid upfront).
1. Write a linear equation to compute the amount Tom's
brother must
pay if he wishes to rent Tom's catnip for x days.
2. Use your equation to determine how much Tom's brother
must pay
Tom to rent the catnip for seven days.
| Prev | Next |