Math 366 Practice Problems for Exam 2
1.Constructive Proof of an Existential Statement.
(a) Prove that there is an even integer n such that n mod 3 = 1.
(b) Prove that there exists a rational number q such that 9 q2 = 4.
(c) Prove that there exist two real numbers whose product is less than their
sum .
(d) Prove that there exist two real numbers which are not equal to each other
and whose product
is equal to their sum .
(e) Prove that there is an odd integer n such that n > 1 and n has the form 3k +
1 for some
integer k.
2. Direct Proof of a Universal Statement.
(a) Prove that if n is an integer which is divisible by 6 then n is divisible by
3.
(b) Prove that for any integers a, b, c, and d, if a divides b and c divides d
then a · c divides b · d.
(c) Prove that the product of two odd integers is odd.
(d) Prove that for any sets A, B, and C, if A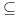 
B and A
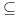C then A
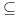B ∩ C.
(e) Prove that if n is an integer which is divisible by 5 then 3n is divisible
by 15.
(f) Prove that for any rational numbers a and b, if a ≠ 0 then there is a
rational number x such
that ax + b = 0.
(g) Show that the reciprocal of any nonzero rational number is rational.
3. Proof by Cases.
(a) Prove that for every integer n, n and n + 2 have the same parity (i.e.
either n and n + 2 are
both even or n and n + 2 are both odd).
(b) Prove that for any integer n, n2 + n is even.
(c) Prove that for any integers n and m, n2+3m ≠ 2. Hint: Use an argument by
cases depending
on what the remainder is when n is divided by 3.
(d) Prove that for any sets A, B, and C, if A
C then A ∪ (B ∩ C)
C.
4. Mathematical Induction .
(a) Prove that for any integer n, if n ≥ 0 then 4 divides 5n -
1.
(b) Prove that for any integer n, if n ≥ 1 then 4 divides 6n - 2n.
(c) Show that 2n + 1 < 2n for every integer n with n ≥ 3.
(d) Using the fact that 2n+1 < 2n for every integer n with n ≥ 3, show that for
every integer n,
if n ≥ 5 then n2 < 2n.
5. Strong Mathematical Induction and the Well- Ordering Principle .
(a) Suppose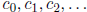 
is a sequence defined as follows:
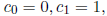
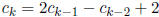for all integers k ≥ 2.
Prove that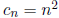 
for all integers n ≥ 0.
(b) Suppose 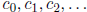is a sequence defined as follows:
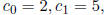
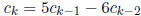for all integers k ≥ 2.
Prove that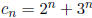 
for all integers n ≥ 0.
6. Proofs by Contradiction and Contraposition.
(a) Prove that there is no smallest real number x such
that 1 < x < 2..
(b) For any integer n, if n2 is not divisible by 3 then n is not
divisible by 3.
7. Computations with Sets.
(a) Let A = {a, c, d} and B = {b, c, f} be subsets of the universal set U = {a,
b, c, d, e, f, g}.
Compute A ∪ B, A ∩ B, A − B, Ac, and A × B using “bracket” notation.
(b) Let A = {1, 3} and B = {2, 3} be subsets of the universal set U = {0, 1, 2,
3, 4}. Compute
A ∪ B, A ∩ B, A − B, Ac, and A × B using “bracket” notation.
| Prev | Next |