Math 142 Exam 1 Practice Problems
Exam 1 may include problems similar to these. This is not
meant to represent the only types
of problems that will be on the exam. It is also not representative of the
length of the exam.
It just gives you a sample of the nature and level of difficulty of the problems
that will be on
the exam.
1. Find the antiderivatives of the following functions:
(a)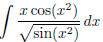 
(answer:
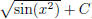) (hint: use substitution )
(b)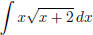 
(answer:
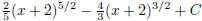) (hint: use substitution )
(c)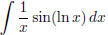 
(answer: -cos(ln x) + C) (hint: use
substitution)
(d)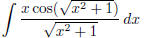 
(answer:
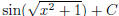) (hint: use substitution)
(e)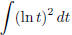 
(answer:
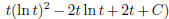) (hint: use integration by parts on
)
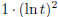(f)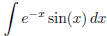 
(answer:
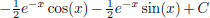(hint: use integration by parts)
(g)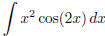 
(answer:
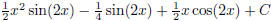) (hint: use integration
by parts)
(h)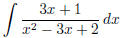 
(answer:
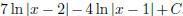) (hint: use partial fraction decom -
position)
(i)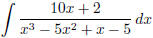 
(answer:
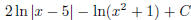) (hint: use partial fraction
decomposition)
(j)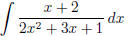 
(answer:
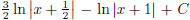) (hint: use partial fraction
decomposition)
(k)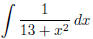 
(answer:
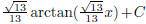) (hint: use fact that
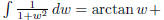
C)
(l)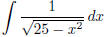 
(answer:
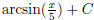) (hint: use fact that
)
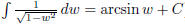(m)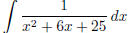 
(answer:
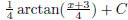) (hint: complete the square )
(n)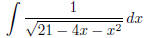 
(answer:
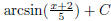) (hint: complete the square )
(o)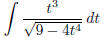 
(answer:
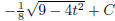) (hint: use substitution)
(p)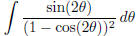 
(answer:
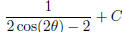) (hint: use substitution)
(q)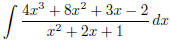 
(answer:
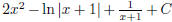) (hint: use long division and
then partial fraction decomposition)
(r)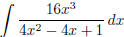 
(answer:
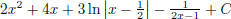) (hint: use long division
and then partial fraction decomposition )
(s)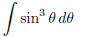 
(answer:
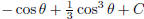) (hint: 
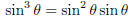n
)
(t)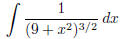 
(answer:
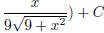) (hint: use trigonometric substituion )
2. (a) What is the exact value of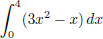 
(answer:
56)
(b) Find LEFT(2), RIGHT(2), MID(2), TRAP(2), SIMP(2) (answer: 20, 108, 52, 64,
56)
3. Calculate the following improper integrals
(a)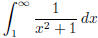 
(answer: converges to
)
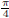(b)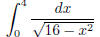 
(answer: converges to
)
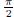(c)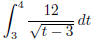 
(answer: converges to 24)
(d)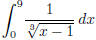 
(answer: converges to
)
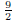(e)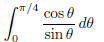 
(answer: diverges)
4. Investigate the convergence or divergence of the following integrals. Justify
your answer using the
comparison test .
(a)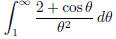 
(answer: converges)
(b)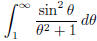 
(answer: converges)
(c)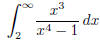 
(answer: diverges)
(d)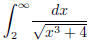 
(answer: converges)
5. Write a Riemann sum and then a definite integral representing the area of the
region, using the strip
shown. (answer: 9π )
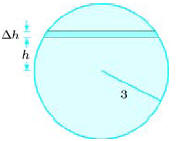
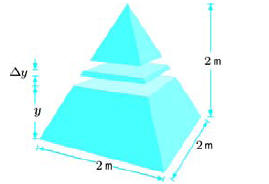
6. Write a Riemann sum and then a definite integral
representing the volume of the solid, using the strip
shown. (answer: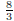 
)
7. The region bounded by the curve y = x2 and the x-axis
between x = 0 and x = 1 is revolved around
the horizontal line y = 10. Find the volume of this solid of revolution.
(answer: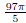 
)
8. The region bounded by the curve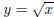 
and the
x-axis between x = 0 and x = 1 is revolved around
the vertical line x = 1. Find the volume of this solid of revolution. (answer:
)
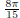9. Find the arc length of the graph of the function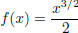 
from x = 0 to x = 1. (answer: 
)
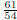10. Find the area inside the circle r = 1 and outside the cardioid r = 1 - cosθ
(answer: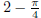 
)
11. Find the area lying outside r = 3 sinθ and inside r = 1 + sinθ .
(answer: π)
12. A rod with density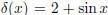 
lies on the x-axis
between x = 0 and x = π . Find the center of
mass of the rod. (answer: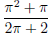 
)
13. A rod with density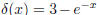 
lies on the x-axis
between x = 0 and x = 2. Find the center of mass
of the rod. (answer: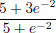 
)
14. A metal plate with constant density 5 gm/cm3 has a shape bounded by the
curve 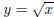and the
x-axis with 0 ≤ x ≤1 and x, y in cm.
(a) Find the total mass of the plate. (answer:
)
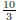(b) Find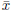 
(answer: 
)
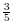| Prev | Next |