Basic Algebra Review for Math 1441
0 Introduction On your first day of Math 1441, you
will take a Basic Algebra Exam.
You should pass this exam in order to stay in the course. This material will
help you review
this elementary material in advance of the first day. If you cannot master these
algebra skills ,
you should instead take Math 1400. These skills and more advanced skills will be
heavily
used in Math 1441.
1 Slope
Recall that slope m is defined as
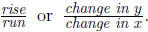Rise is the distance traveled vertically
and is positive if traveling up (in the positive y direction). Run is the
distance traveled
horizontally and is positive if traveling right (in the positive x direction).
We estimate the
slope of a line by drawing horizontal and vertical lines and estimating rise and
run.
Example: Approximate the slope of the given line.
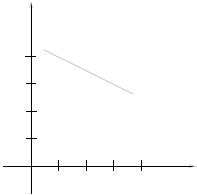
Solution: We draw in horizontal and vertical lines and estimate the run as 2 and
the rise as
-1. This gives an approximate slope of - 1/2.
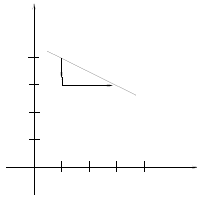
Note: If we had traveled in the other direction, we would estimate the run to be
-2 and the
rise to be 1, giving the same answer of - 1/2.
Try the following problems. The answers are in the solution section .
1. Approximate the slope of the given line:
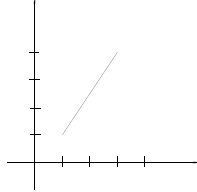
2. Approximate the slope of the given line:
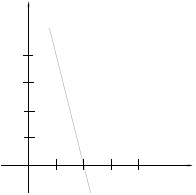
2 Lines
A line which goes through points (x1, y1) and (x2, y2)
has slope
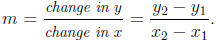
If a line has slope m and goes through point (x1, y1), we call an arbitrary
point on the line
(x; y) and get that
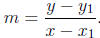Rewriting, we get the usual form y - y1 = m(x - x1).
Example: Find the line through points (2, -3) and (1,4):
The slope is
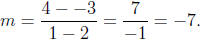To nd the equation, we can use either point. Using
the point (2,-3), we get y - -3 = -7(x - 2).
The equation of the line with slope m and y intercept b is
y - b = m(x - 0) or y = mx + b.
(Recall: Since points on the y axis have x = 0, a y intercept of b indicates
that point (0; b)
is on the line.)
Try the following problems. Recall that parallel lines have the same slopes. The
answers are
in the solutions section.
1. Find the equation of the line through points (4,-2) and (-1, 3).
2. Find the equation of the line with x intercept 3 and y intercept -2.
3. Find the equation of the line that goes through the point (2; 3) and is
parallel to the
line 2x + 6y = 1.
3 Exponents
When you get confused about the rules for exponents , think about what the exponent means.
Example: x4x2 = (xxxx)(xx) = xxxxxx = x6. The exponents are added.
Example: (x4)2 = (x4)(x4) = (xxxx)(xxxx) = xxxxxxxx = x8. The exponents are multiplied.
Example:
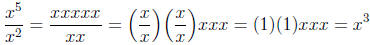. The exponents are subtracted .
Example:(xy)2 = (xy)(xy) = xxyy = x2y2. In general, (xy)n = xnyn.
Beware: (x+y)2 ≠ x2+y2 since (x+y)2 = (x+y)(x+y) = x2+xy+xy+y2 = x2+2xy+y2
Summary of Rules of Exponents:
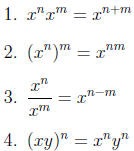
Example:
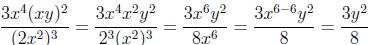
Try the following problems, simplifying completely and writing answers with no
negative
exponents. The answers are in the solution section.
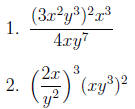
4 Negative and Fractional Exponents
We will use the rules of exponents in the above section to understand what
negative and
fractional exponents mean.
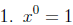Why?
Why?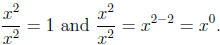 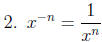Since
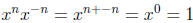, we know
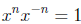. When we divide both sides by
,
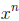we get
.
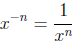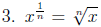Why?
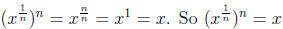and we
take the nth root of both sides to get
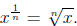
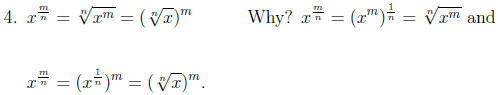
Example: Write
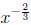without fractions or negatives in the exponent:
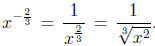
Another correct answer would be
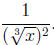
Example: Write
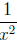in the form
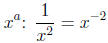
Example: Write
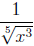in the form
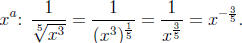
Try the following problems. The answers are in the solution section.
1. Write
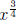without fractions or negatives in the exponent.
2. Write
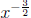without fractions or negatives in the exponent.
3. Write
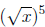in the form
.
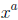4. Write
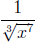in the form
.
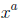5 Fractions
We'll look at some numerical examples first. For each example, try it yourself
before you
look at the solution.
Example:
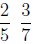Answer :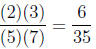
Example: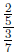
Answer:
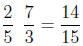
Example:
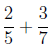Answer :
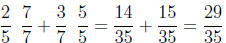
Now let's try some examples with variables . Try yourself before looking at
answers.
Example:
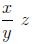Answer: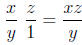
Example:
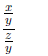Answer:
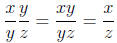
Example:
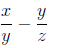Answer:
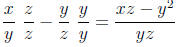
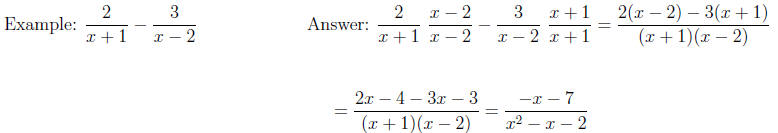
Try the following problems. The answers are in the solution section.
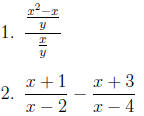
| Prev | Next |