Ancient Greek Algebra

What the Greeks did in the area of algebra is subtle , so subtle that one may well debate whether they
did anything at all in this area. Apart from one tantalizing reference to a problem that is algebraic in
nature, it is very difficult to find anything that deserves the name before the time of Diophantus in the
third century CE. The one exception is a reference to a problem that was apparently stated during the time
of Plato. All that is known about it is the following. In his commentary on Nicomachus’ Introduction
to Arithmetic Iamblichus presents an obscurely worded technique that he ascribes to one Thymaridas,
which the nineteenth-century philologist Georg Heinrich Ferdinand Nesselmann (1811–1881) was able to
elucidate. This technique solves the problem of determining a number of quantities, given the sum of all of
them and the sum of a fixed one with each of the others. Iamblichus called this technique the epanthema
(blossom, that is, full development) of Thymaridas.

The general focus of Euclid’s thirteen books is geometric, with an interruption in Books 7–9 to discuss
number theory. To find algebra in this treatise one has to interpret the results suitably. The main place to
look is in Book 2, which is a short book, containing only 14 propositions. The first ten of these do look like
algebraic propositions clothed in geometric language. For example, Proposition 1 asserts what we would
call the distributive law for multiplication : If one of two lines is divided , the rectangle on the two lines
is (the sum of ) the rectangle on each of the parts and the undivided line. We would interpret this
proposition as saying 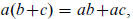but that is our language, not Euclid’s. The “algebra” (if that is what
it is) gets more complicated. Proposition 5, for example, asserts that If a line is divided into equal and
unequal parts, then the square on the equal parts equals (the sum of ) the rectangle on the two parts
and the square on the segment between the two points of division. If the two unequal parts are a and b,
we would rewrite this statement as the basic identity for solving quadratic equations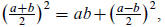
which, as we have seen, was a fundamental principle used in the cuneiform tablets. Proposition 9 asserts
what we would call the parallelogram law: If a line is divided into equal and unequal parts, the (sum
of ) the squares on the unequal parts equals twice the (sum of ) the square on the half and the square
on the segment between the two points of division. That is, 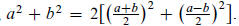Up to
this point, it appears that the Greeks are merely using geometric language to do what was done numerically
by the Mesopotamian mathematicians; and it is natural to suppose that they did so because square roots fit
smoothly into geometry, but not so smoothly into arithmetic. The view that this book is basically algebraic in
character is associated with the Danish historian of mathematics Hieronymus Georg Zeuthen (1839–1920).
It must be said that these first ten propositions of Book 2 do lend themselves to that interpretation.

The last four propositions are applications of these ten propositions, however, and they do not suggest
algebra at all. Proposition 11 is a construction problem: to divide a line so that the rectangle on the
whole and one of the parts equals the square on the other part, that is, to divide the line in mean
and extreme ratio. This problem does not have any obvious algebraic source that needed to be recast as
geometry. It does, however, use the previous propositions. Propositions 12 and 13 give what we now call
the law of cosines for obtuse- and acute-angled triangles respectively, in the form that the square on the
side opposite the obtuse angle exceeds the sum of the squares on the other two sides by the rectangle on
one of the sides and the length of the projection of the other side on its extension outside the obtuse angle.
For an acute angle the excess is a deficiency and the projection falls inside the angle. The fourteenth and
final proposition of the book, which shows how to construct a square equal to any polygon, also has a very
obvious geometric source and also makes use of the previous propositions.

We conclude that if Euclid was intending to do algebra geometrically, he kept his intention well hidden.
His applications of the “geometric algebra” in Book 2 are topics of intrinsic interest in geometry, not algebra
problems disguised as geometry, as is the case in many other cultures. On the other hand, the “application”
problems in Book 6 are less obviously geometric in origin and do map nicely into the problems of finding
two numbers (represented by lines in Euclid’s case) having a prescribed product (rectangle) and sum or
difference, according as the problem is one of application with defect or application with excess. Yet,
once again, Euclid states all these theorems in terms of parallelograms having a prescribed angle, whereas
rectangles with square defect or excess would suffice to represent the algebraic problems. The case that
Euclid’s geometry contains algebra in disguised form is difficult to make.

A somewhat better case can be made in the number-theoretic books, where at least numbers are reasoned
on as abstractions. The algebraic spirit is there, but the focus is on studying the intrinsic properties
of numbers, not on finding numbers satisfying certain conditions in relation to other numbers. For example,
in Proposition 12 of Book 7, it is proved that if two numbers are such that when the smaller is continuously
subtracted from the larger the remainder is never equal to its predecessor until the number 1 is reached, then
the numbers are relatively prime, that is, not both divisible by any integer larger than 1. The proof consists of
showing that if a number divides both numbers, then it divides their difference; and conversely if it divides
the difference and one of the two numbers , then it divides both numbers. The assumption of a larger divisor
than 1 then leads to the impossibility that the number 1 is divisible by a larger number. In the proof, the
numbers are called AB and as if they were intended to be represented by line segments. The reasoning
does not depend on any such mental picture, yet the author seemed to have thought it was needed. Was it
really such a radical , counterintuitive step to use an abstract symbol to represent an unspecified number?
The first record of such a step being taken in Greek mathematics came at least 500 years after Euclid, in the
work of Diophantus discussed in the Chapter 14.

The Post-Euclideans. Algebra is now universally used to discuss conic sections in analytic geometry
and calculus courses, and some historians have argued that the work of Apollonius himself is basically
algebraic. Certainly that is the impression one would get from reading the translations of it given by Heath,
who took it on himself to save the modern reader time by translating everything into modern algebraic
symbolism. One must be wary of seeming familiarity in historical documents, however. As Jacob Klein
(1968, p. 5) says, “most of the standard histories attempt to grasp Greek mathematics itself with the aid of
modern symbolism, as if the latter were an altogether external ‘form’ which may be tailored to any desirable
‘content.’ ” Precisely! To translate in this case is to betray. It is true that the locus description of a conic
section as given by Apollonius, which involves reference to two fixed, mutually perpendicular lines, is
very easily translated into what we now call the equation of the curve . That fact by no means implies that
Apollonius thought of them in that way. Indeed, all his complicated Euclidean-style proofs loudly proclaim
the exact opposite.

If we look at the work of other later geometers like Heron, who does write prescriptions that amount
to formulas , it is still difficult to discern any attempt to determine (the length of) an unknown line from
its position in a figure. Heron seems to be concerned with measurement but not the solution of problems
leading to equations.

The ancient Greek writer most often credited with doing algebra—indeed, the Renaissance mathematicians
credited him with creating it—was Diophantus. That verdict, however, is disputed by Jacob Klein
(1899–1978) in very thorough and interesting study of Greek mathematics (Klein, Jacob, 1968 ). This work
is discussed in Chapter 14 of the text in connection with the work of Diophantus. Here we merely note
that in our discussion (Sect. 11.1 of the text) of what Pappus called analysis we mentioned that the process
he described—imagining a construction completed and seeing how its properties determine what it must
be—was precisely algebra when the object of contemplation was numerical. For Pappus, of course, it was
not numerical, and hence his analysis was not algebra. That point lies at the heart of Klein’s argument, as
we shall see in the next chapter.

Literature
Klein, Jacob, 1934–1936. Greek Mathematical Thought and the Origin of Algebra, translated by Eva
Brann, MIT Press, Cambridge, MA, 1968.