A Math Primer
Exponents and Roots
A. Exponents
Definition
In xn, x is the base, and n is the exponent (or power)
We defined positive integer powers by
xn = x · x · x · . . . · x (n factors of x)
Properties
The above definition can be extended by requiring
other powers (i.e. other than positive integers) to
behave like the positive integer powers. For example,
we know that
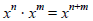
for positive integer powers, because we can write out
the multiplication.
Example:
x2 x5 = (x · x)(x · x · x · x · x)
=
x · x · x · x · x · x · x = x7
We now require that this rule hold even if n and m
are not positive integers, although this means that we
can no longer write out the multiplication (How do
you multiply something by itself a negative number
of times? Or a fractional number of times?).
We can find several new properties of exponents by
similarly considering the rule for dividing powers :
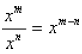
This rule is quite reasonable when m and n are
positive integers and m > n. For example:
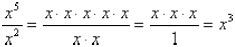
where indeed 5 – 2 = 3.
However, in other cases it leads to situations where
we have to define new properties for exponents.
First, suppose that m < n. We can simplify it by
canceling like factors as before :
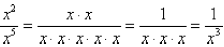
But following our rule would give
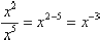
In order for these two results to be consistent, it must
be true that
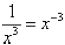
or, in general,
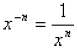
Notice that a minus sign in the exponent does not
make the result negative—instead, it makes it the
reciprocal of the result with the positive
exponent.
Now suppose that n = m. The fraction becomes
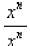
which is obviously equal to 1. But our rule gives
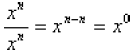
Again, in order to remain consistent we have to say
that these two results are equal, and so we define
x0 = 1
for all values of x (except x = 0, because 00 is
undefined)
Summary of Exponent Rules
The following properties hold for all real numbers x,
y, n, and m, with these exceptions:
1. 00 is undefined
2. Dividing by zero is undefined
3. Raising negative numbers to fractional powers
can be undefined
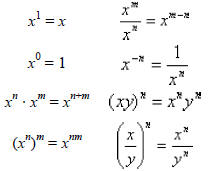
B. Roots
Definition
Roots are the inverse of exponents. An nth root
“undoes” raising a number to the nth power, and
vice-versa. (The correct terminology for these types
of relationships is inverse functions, but powers and
roots can only be strictly classified as inverse
functions if we take care of some ambiguities
associated with plus or minus signs, so we will not
worry about this yet). The common example is the
square root , which “undoes” the act of squaring. For
example, take 3 and square it to get 9. Now take the
square root of 9 and get 3 again. It is also possible to
have roots related to powers other than the square.
The cube root , for example, is the inverse of raising
to the power of 3. The cube root of 8 is 2 because 23
= 8. In general, the nth root of a number is written:
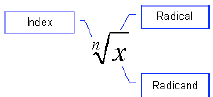
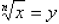if and only if
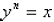
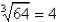because 43 = 64
We leave the index off the square root symbol only
because it is the most common one. It is understood
that if no index is shown, then the index is 2.
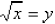if and only if
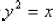
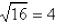because 42 = 16
Square Roots
The square root is the inverse function of squaring
(strictly speaking only for positive numbers, because
sign information can be lost)
Principal Root
Every positive number has two square roots, one
positive and one negative
Example: 2 is a square root of 4 because 2 x 2 = 4,
but –2 is also a square root of 4 because (–2) x
(–2) = 4
To avoid confusion between the two we define the
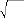symbol (this symbol is called a radical ) to
mean
the principal or positive square root.
The convention is: For any positive number x,
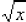is the positive root, and
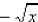is the negative root.
If you mean the negative root, use a minus sign in
front of the radical.
Example:
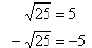
| Prev | Next |